Trigonometrische Funktionen
Inhaltsverzeichnis
\(\\\)
Einheitskreis
Winkelfunktionen für den Einheitskreis
Betrachten wir ein rechtwinkliges Dreieck mit einem Winkel \(\alpha\) und einer Hypothenuse mit der Länge \(1\),
\(\quad\)

so gilt:
\(\quad\) \( \begin{array}{ l c c c c c l } \color{blue}{sin(\alpha)} & = & \frac{Gegenkathete}{Hypothenuse} & = & \frac{Gegenkathete}{1} & = & \color{blue}{Gegenkathete} \\[8pt] \color{#CC0000}{cos(\alpha)} & = & \frac{Ankathete}{Hypothenuse} & = & \frac{Ankathete}{1} & = & \color{#CC0000}{Ankathete} \\ \end{array} \)
\(\\\)
Mit dieser Beschreibung der beiden Winkelfunktionen ergibt sich nun
\(\quad\) \( \begin{array}{ l c c c l } tan(\alpha) & = & \frac{\color{blue}{Gegenkathete}}{\color{#CC0000}{Ankathete}} & = & \frac{\color{blue}{sin(\alpha)}}{\color{#CC0000}{cos(\alpha)}} \end{array} \)
\(\\[1em]\)
Sinus im Einheitskreis
Legen wir dieses Dreieck in den Einheitskreis, ein Kreis mit dem Radius 1, so können wir erkennen, dass der Sinus von \(\alpha\), also der gleiche \(y\)-Wert, darin zweimal vorkommt.
\(\quad\)
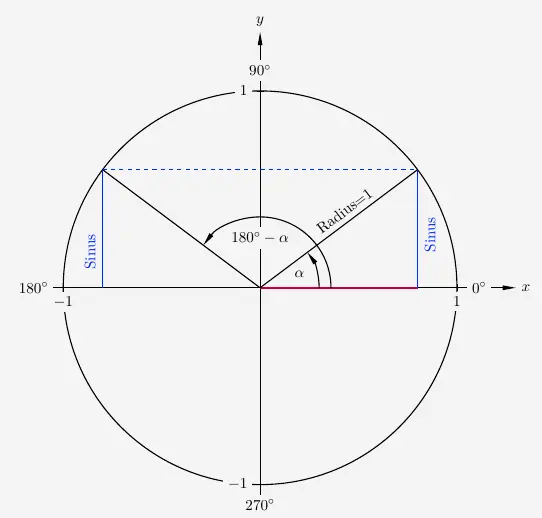
Daraus ergibt sich
\(\quad\) \( \begin{array}{ l c c c l } sin(\alpha) & = & sin(180^{\circ}-\alpha) \end{array} \)
\(\\[1em]\)
Kosinus im Einheitskreis
Ebenso ergeben sich zwei Winkel mit dem gleichen Kosinus von \(\alpha\), dem gleichen \(x\)-Wert.
\(\quad\)
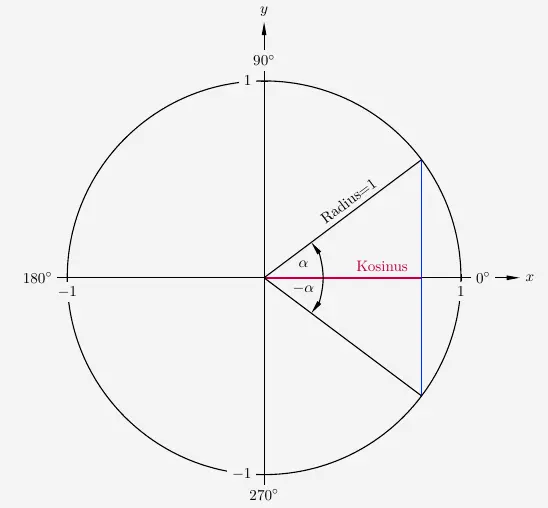
Es gilt:
\(\quad\) \( \begin{array}{ l c c c l } cos(\alpha) & = & cos(-\alpha) \end{array} \)
\(\\[1em]\)
Tangens im Einheitskreis
Um den Tangens graphisch darzustellen, werden links und rechts an den Einheitskreis senkrecht zwei Tangenten gelegt. Verlängern wir nun die Hypothenuse bis sie an die Tangente stößt, erhalten wir den Tangens von \(\alpha\).
\(\quad\)

Gemäß der Darstellung erhalten wir
\(\quad\) \( \begin{array}{ l c l } tan(\alpha) & = & tan(\alpha + 180^{\circ}) \end{array} \)
\(\\\)
Außerdem gilt für alle drei Winkelfunktionen
\(\quad\) \( \begin{array}{ l c l } sin(\alpha) & = & sin(\alpha + 360^{\circ}) \\[5pt] cos(\alpha) & = & cos(\alpha + 360^{\circ}) \\[5pt] tan(\alpha) & = & tan(\alpha + 360^{\circ}) \\ \end{array} \)
\(\\[2em]\)
Von der Winkelfunktion zur trigonometrischen Funktion
Um eine trigonometrische Funktion zu erhalten, muss die Winkelfunktion \(sin(\alpha)\), \(cos(\alpha)\) oder \(tan(\alpha)\) auf ein kartesisches Koordinatensystem übertragen werden. Zur Veranschaulichung ist der Sinus dafür am besten geeignet. Die Winkel werden dazu auf der \(x\)-Achse abgetragen und die \(y\)-Werte vom Einheitskreis übernommen.
\(\quad\)

Hier sind die zu der trigonometrischen Funktion gehörenden Punkte für die Winkel 15°, 30°, 45° und 60° dargestellt. Werden nun alle Winkel des Einheitskreises auf das kartesische Koordinatensystem übertragen, so entsteht der obige Graph der Sinusfunktion im Intervall \([ 0^\circ ; 360^\circ ]\).
\(\\[1em]\)
Trigonometrische Funktionen im Bogenmaß
Es ist jetzt nicht üblich, Punkte im kartesischen Koordinatensystem mit Winkelangaben zu versehen, also zum Beispiel den zweiten Punkt als \((30^\circ | 0{,}5 )\) zu schreiben. Winkelangaben werden nur nur im Polarkoordinatensystem (Winkelangabe und Radius) gemacht, das beispielsweise in dem Gebiet komplexe Zahlen verwendet wird.
Statt dem Winkel wird im kartesischen Koordinatensystem das Bogenmaß, also die Länge des Bogens, die sich im Einheitskreis aus dem Winkel ergibt.
\(\quad\)
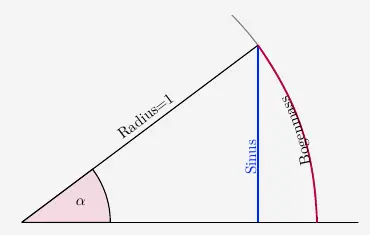
Das Bogenmaß von \(360^\circ\) ist der Umfang des Einheitskreises mit
\(\quad\) \( U \; = \; 2 \pi r \; = \; 2 \pi \cdot 1 \; = \; 2 \pi \)
\(\\[1em]\)
Sinusfunktion und Kosinusfunktion im Bogenmaß
Es ergibt sich damit die folgende Einteilung der Sinusfunktion:
\(\quad\)
Entsprechend lässt sich auch die Kosinusfunktion mit den Werten aus dem Einheitskreis darstellen.
\(\quad\)
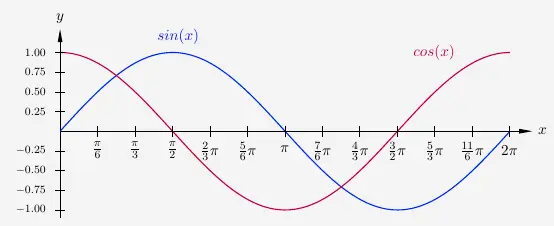
Es ist leicht zu erkennen, dass der Graph Kosinusfunktion identisch ist mit dem Graphen der Sinusfunktion, jedoch um \(\frac{\pi}{2}\) nach links verschoben. Es gilt
\(\quad\) \( cos(x) \; = \; sin \left( x + \frac{\pi}{2} \right) \)
\(\\[2em]\)
Eigenschaften trigonometrischer Funktionen
Einige wesentliche Eigenschaften heben die trigonometrischer Funktionen von anderen Funktionstypen ab.
Periodizität
Trigonometrische Funktionen weisen stets ein periodisches Verhalten auf, weswegen sie auch als periodische Funktionen oder als zyklische Funktionen bezeichnet werden.
\(\\[1em]\)
Sinusfunktion als periodische Funktion
\(\quad\)
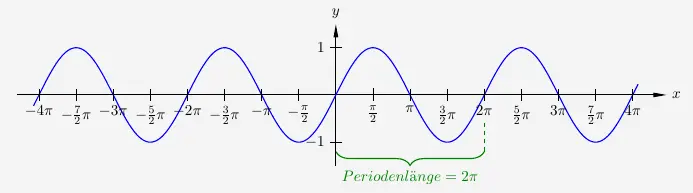
Die Funktion
\(\quad\) \( f(x) \; = \; sin(x) \)
ist punktsymmetrisch zum Koordinatenursprung.
\(\\\)
Auffallend ist, dass der Graph in \(x\)-Richtung unbegrenzt ist, jedoch in \(y\)-Richtung eindeutige Grenzen aufweist. Es gelten der
\(\quad\) \( \begin{array}{ c c l } \qquad \text{Definitionsbereich} & : & \mathbb{D} \; = \, \mathbb{R} \end{array} \)
und der
\(\quad\) \( \begin{array}{ c c l } \qquad \text{Wertebereich} & : & \mathbb{W} \, = \, [ -1 \, ; \, 1 ] \end{array} \)
\(\\\)
Ferner ist zu erkennen, dass es unendlich viele Nullstellen gibt. Diese sind bei \(sin(x)\), \(cos(x)\) und \(tan(x)\) zugleich auch die Wendestellen. Die Nullstellen treten immer in Abständen von der halben Periodenlänge auf, sind also Vielfache von \(\pi\), und werden beschrieben mit
\(\quad\) \( \begin{array}{ r c l } \text{Nullstellen} \; = \, \{ x \, | \, x \, = \, k \cdot \pi \, , \; k \in \mathbb{Z} \} \\ \end{array} \)
\(\\\)
Ebenfalls gibt es unendlich viele Extremstellen, die in Abständen einer ganzen Periodenlänge auftreten. Es gilt:
\(\quad\) \( \begin{array}{ c c l } \text{Hochpunkte} & = & \{ x \, | \, x \, = \, \frac{\pi}{2} + k \cdot 2 \pi \, , \; k \in \mathbb{Z} \} \\[8pt] \text{Tiefpunkte} & = & \{ x \, | \, x \, = \, - \frac{\pi}{2} + k \cdot2 \pi \, , \; k \in \mathbb{Z} \} \\ \end{array} \)
\(\\\)
Zusammengefasst:
\(\quad\)

\(\\[1em]\)
Kosinusfunktion als periodische Funktion
\(\quad\)

Die Funktion
\(\quad\) \( f(x) \; = \; cos(x) \)
ist achsensymmetrisch zur \(y\)-Achse.
Die Nullstellen, Extremstellen und Wendestellen sind jeweils um \(-\frac{\pi}{2}\) im Vergleich zu \(sin(x)\) verschoben.

\(\\[1em]\)
Tangensfunktion als periodische Funktion
\(\quad\)

Die Funktion
\(\quad\) \( f(x) \; = \; tan(x) \)
ist punktsymmetrisch zum Koordinatenursprung und ebenfalls eine periodische Funktion.
Die Tangensfunktion ist eine unstetige Funktion. Das heißt, dass sie nicht aus einem Linienzug gezeichnet werden kann. Denn sie weist periodisch wiederkehrend Stellen auf, in denen sie nicht definiert ist. Diese Definitionslücken heißen Polstellen oder Pole. Linksseitig der Polstellen strebt die Funktion gegen \(\infty\) und rechtsseitig der Polstellen gegen \(-\infty\). Das wiederum bedeutet, dass an den Polstellen eine Sprungverhalten zu verzeichnen ist.
\(\quad\)
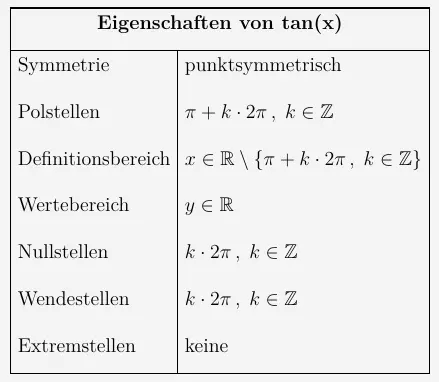
Die Tangensfunktion ist hier nur der Vollständigkeit halber aufgeführt und wird im Folgenden nicht weiter behandelt.
\(\\[2em]\)
Transformationen trigonometrischer Funktionen
Weitere Eigenschaften der trigonometrischen Funktionen ergeben sich durch die Transformationen
- Streckung/Stauchung
- Verschiebung
- Spiegelung
Diese wurden in den Beiträgen Streckung von Funktionen, Verschieben von Funktionen und Spiegelung von Funktionen schon beschrieben, werden hier aber noch weiter ausgeführt.
\(\\[1em]\)
Allgemeine Gleichung der Sinusfunktion
\(\quad\) \( \boxed{f(x) \; = \; a \cdot sin \Big( b \cdot (x -c) \Big) +d} \)
Gelegentlich sieht man auch die Gleichung
\(\quad\) \( f(x) \; = \; a \cdot sin \big( b \cdot x -c \big) +d \)
Hierbei sind die Berechnungen der Transformationen aber etwas komplizierter. Deshalb verwenden wir im Folgenden die erste (eingerahmte) Gleichung.
Die Parameter haben nun folgende Bedeutung:
a: Amplitude
b: Frequenz/Periodenlänge
c: Verschiebung in \(x\)-Richtung
d: Verschiebung in \(y\)-Richtung
\(\\\)
Betrachten wir ein Beispiel aus der Physik, eine Feder, an der eine Kugel befestigt ist.
\(\quad\)

Ziehen wir die Kugel aus der Ruhelage ein Stück nach unten und lassen los, so beginnt die Kugel im zeitlichen Verlauf in Form einer Sinuskurve (oder Kosinuskurve) zu schwingen, sofern hier jede Reibung vernachlässigt wird. Den Ausschlag nach oben und unten nennt man die Amplitude der Schwingung.
\(\\[1em]\)
Amplitude
\(\quad\)

Der Parameter \(a\) gibt hier die Amplitude an und bewirkt eine Streckung (oder auch Stauchung) der Sinusfunktion in \(y\)-Richtung.
\(\\[1em]\)
Höhenverschiebung und Amplitude
Parameter \(d\) gibt die Ruhelage einer Schwingung, oder in diesem Fall besser gesagt die Null-Linie der Funktion an.
\(\\\)
Wie werden nun die Graphen der Funktionen
\(\quad\) \( \begin{array}{ r c l} f(x) & = & 0{,}5 sin(x) + 2 \\[6pt] g(x) & = & 1{,}5 sin(x) - 1 \\ \end{array} \)
gezeichnet?
\(\\\)
Dazu gehen wir folgendermaßen vor:
-
Zunächst zeichnen wir die \(x\)-Achse mit der Einteilung \(\frac{\pi}{2}\), \(\pi\), \(\frac{3}{2} \pi\) und \(2 \pi\).
-
Für die \(y\)-Achse brauchen wir den Bereich von \(-2\) bis \(3\).
-
Wir zeichnen die Null-Linie ein.
-
Auf der Null-Linie setzen wir Punkte an den Stellen \(0\), \(\pi\), und \(2 \pi\).
-
An der Stelle \(\frac{\pi}{2}\) setzen wir Markierungen oberhalb der Null-Linie mit der angegeben Amplitude für die Hochpunkte und an der Stelle \(\frac{3}{2} \pi\) unterhalb der Null-Linie mit der angegeben Amplitude für die Tiefpunkte.
-
Nun können wir die Graphen zeichnen.
\(\quad\)
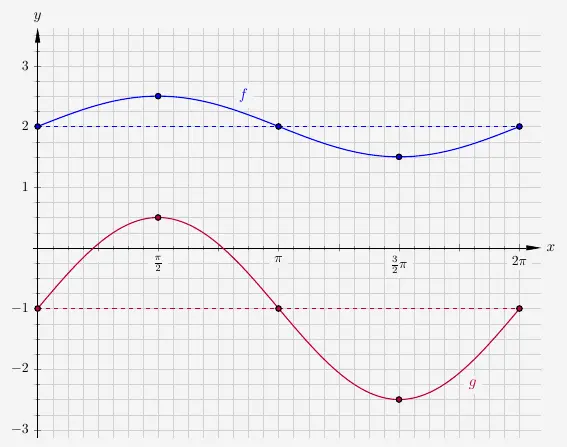
\(\\\)
Der Graph von \(g\) schneidet nun die \(x\)-Achse. Wie können die Nullstellen jetzt bestimmt werden? Um mit dem Taschenrechner mit trigonometrischen Funktionen zu rechnen, muss der Taschenrechner auf Bogenmaß umgestellt werden. Das funktioniert mit dem Casio fx-991 DE X wie folgt:
\(\quad\)
\(\boxed{\color{#C19A6B}{SHIFT}} \; \boxed{MENU}\)
Es erscheint
\(\quad\)

Wir wählen \(\boxed{2}\)
\(\quad\)

und noch einmal \(\boxed{2}\) für Bogenmaß. Auf dem Taschenrechner steht jetzt ein \(R\) für Radiant. Auf dem gleichen Weg kann man nach den Berechnungen wieder auf Grad umstellen.
Es gilt für die Nullstellenberechnung:
\(\quad\) \( \begin{array}{ r c l c l} g(x) & = & 0 \\[16pt] 1{,}5 sin(x) - 1 & = & 0 & \; | +1 \\[6pt] 1{,}5 sin(x) & = & 1 & \; | :1{,}5 \\[6pt] sin(x) & = & \frac{2}{3} \\[12pt] x_1 & = & sin^{-1}\left(\frac{2}{3}\right) \\[8pt] x_1 & = & 0{,}728 \\ \end{array} \)
\(\\\)
Um die zweite Nullstelle zu erhalten, verwenden wir die die Formel aus dem Sinus im Einheitskreis:
\(\quad\) \( \begin{array}{ l c l } sin(\alpha) & = & sin(180^{\circ}-\alpha) \end{array} \)
Übersetzt ins Bogenmaß, heißt das:
\(\quad\) \( \begin{array}{ l c l } sin(x) & = & sin(\pi - x) \end{array} \)
\(\\\)
Damit ist
\(\quad\) \( \begin{array}{ l c l } x_2 & = & \pi - x_1 \\[5pt] & = & \pi - 0{,}728 \\[5pt] & = & 2{,}4136 \\ \end{array} \)
\(\\\)
Da die Nullstellen nun alle \(2 \pi\) auftreten ist die vollständige Lösungsmenge der Nullstellen
\(\quad\) \( \quad \begin{array}{ r c l } \mathbb{L} & = & \big\{ 0{,}728 + k \cdot 2 \pi, \, k \in \mathbb{R} \big\} \; \cup \; \big\{ 2{,}4136 + k \cdot 2 \pi, \, k \in \mathbb{R} \big\} \end{array} \)
\(\\[1em]\)
Frequenz und Periodenlänge
Der Parameter \(b\) ist für die Streckung bzw. Stauchung in \(x\)-Richtung verantwortlich und gibt die Frequenz einer Sinusfunktion an. Die Funktion
\(\quad\) \( \begin{array}{ l c l } f(x) & = & sin (3 x ) \end{array} \)
hat demnach
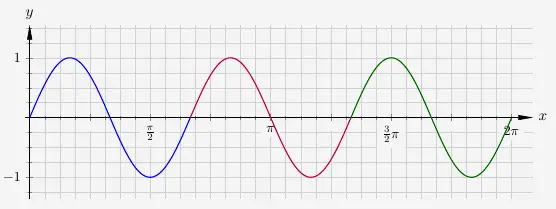
drei Schwingungen (oder besser: drei Perioden des Funktionsgraphen) auf der Länge von \(2 \pi\).
\(\\\)
In der Regel ist es nun aber so, dass sich ganze Perioden nicht gleichmäßig auf \(2 \pi\) verteilen lassen. Deshalb wird meist die Periodenlänge \(p\) als Bezugsgröße genommen. Es gilt
\(\quad\) \( \begin{array}{ l c l } \boxed{ b \; = \; \frac{2 \pi}{p}} \end{array} \)
Bei einer Periodenlänge von \(p=12\)
\(\quad\)
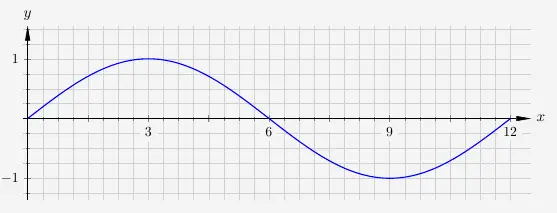
heißt die Funktion
\(\quad\) \( \begin{array}{ r c c c l } f(x) & = & sin \left(\frac{ 2 \pi }{12} x \right) & = & sin \left( \frac{\pi}{6} x \right) \\ \end{array} \)
\(\\[1em]\)
Frequenz und seitliche Verschiebung
Der Parameter \(c\) steht für die seitliche Verschiebung des Graphen der Sinusfunktion. Eine Verschiebung um \(1\) Einheit nach rechts der Funktion
\(\quad\) \( \begin{array}{ l c l } f(x) & = & sin (3 x ) \end{array} \)
\(\quad\)
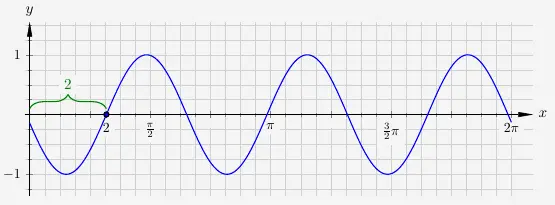
heißt
\(\quad\) \( \begin{array}{ r c l } f(x) & = & sin \big(3 \cdot (x -2)\big) \\ \end{array} \)
Wie hier zu sehen ist, verschiebt sich der Startpunkt der Sinusschwingung auf der \(x\)-Achse.
\(\\[1em]\)
Komplexe Sinusfunktionen zeichnen
Wie nun der Graph der Funktion
\(\quad\) \( \begin{array}{ r c l} f(x) & = & 0{,}5 sin\Big(4 \cdot \big(x - \frac{\pi}{4}\big)\Big) + 2{,}5 \\ \end{array} \)
gezeichnet werden?
\(\\\)
Dazu gehen wir folgendermaßen vor:
-
Zunächst wird ein Koordinatensystem wie abgebildet gezeichnet und beschriftet
\(\quad\)

\(\qquad \qquad \qquad \qquad \quad\)
\(\qquad\) oder aber ausgedruckt. -
Dann zeichnen wir die Null-Linie ein.
-
Die erste Nullstelle liegt entsprechend dem \(c\)-Wert bei \(\frac{\pi}{4}\) auf der Null-Linie. Nach dem \(b\)-Wert gibt es vier Perioden auf der Länge \(2 \pi\). Folglich ist eine Periode \(\frac{\pi}{2}\) lang. Jede halbe Periode kommt eine neue Nullstelle, also in Abständen von \(\frac{\pi}{4}\).
-
Der erste Hochpunkt liegt zwischen den ersten beiden eingezeichneten Nullstellen, also bei \(\frac{3}{8} \pi\) (zwei Kästchen vor \(\frac{\pi}{2}\)), auf der Höhe \(3\). Die Hochpunkte haben einen Abstand von \(\frac{\pi}{2}\) zueinander.
-
Die Tiefpunkte liegen ebenfalls zwischen zwei Nullstellen, jedoch um \(\frac{\pi}{4}\) versetzt zu den Hochpunkten und auf der Höhe \(2\). Die Tiefpunkte haben ebenfalls einen Abstand von \(\frac{\pi}{2}\) zueinander.
-
Gezeichnet sieht alles wie folgt aus:
\(\quad\)
\(\\\)
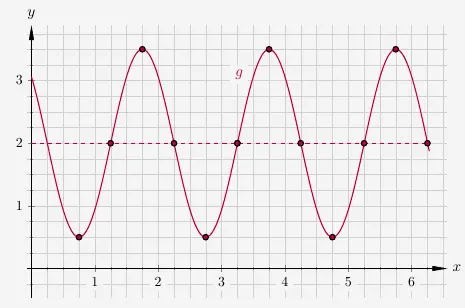
Ein zweites Beispiel:
\(\quad\) \( \begin{array}{ r c l} g(x) & = & 1{,}5 sin\Big( \pi \cdot \big(x - 1{,}25 \big)\Big) + 2 \\ \end{array} \)
-
Zunächst wird ein Koordinatensystem wie abgebildet gezeichnet und beschriftet
\(\quad\)

\(\qquad \qquad \qquad \qquad\)
\(\qquad\) oder aber ausgedruckt. -
Dann zeichnen wir die Null-Linie ein.
-
Die erste Nullstelle liegt entsprechend dem \(c\) -Wert bei \(1{,}25\) auf der Null-Linie. \ Der \(b\) -Wert ist \(\pi\). Die Periodenlänge wird wie folgt berechnet:
\(\qquad\) \( \begin{array}{ c c c c l } b & = & \frac{2 \pi}{p} \\[6pt] \pi & = & \frac{2 \pi}{p} & \, | \, \cdot p \\[6pt] \pi \cdot p & = & 2 \pi & \, | \, : \pi \\[6pt] p & = & 2 \\[6pt] \end{array} \)
\(\qquad\) Jede halbe Periode kommt eine neue Nullstelle, also in Abständen von \(1\).
-
Der erste Hochpunkt liegt zwischen den ersten beiden eingezeichneten Nullstellen, also bei \(1{,}75\) auf der Höhe \(3{,}5\). Die Hochpunkte haben einen Abstand von \(2\) zueinander.
-
Die Tiefpunkte liegen ebenfalls zwischen zwei Nullstellen, jedoch um \(1\) versetzt zu den Hochpunkten und auf der Höhe \(1{,}5\). Die Tiefpunkte haben ebenfalls einen Abstand von \(2\) zueinander.
-
Gezeichnet sieht alles wie folgt aus:
\(\quad\)
\(\\[1em]\)
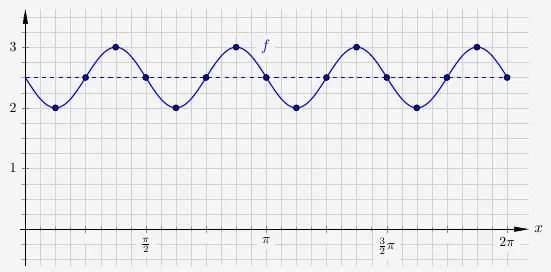
Sinusfunktionen ablesen
Weitaus häufiger als das Zeichnen einer Sinusfunktion wird das Ablesen einer Funktionsgleichung benötigt.
\(\quad\)

Die Vorgehensweise ist ähnlich wie beim Zeichnen. Zuächst bestimmen wir die Null-Linie. Diese befindet sich mittig zwischen den Hoch- und Tiefpunkten. Damit muss \(d=1\) sein.
\(\quad\)
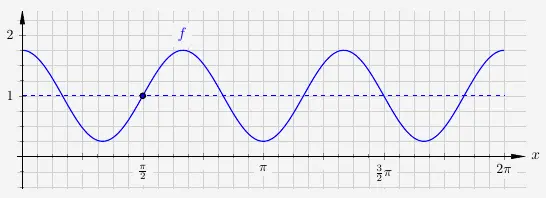
Der Startpunkt der Sinusfunktion befindet sich bei \(\frac{\pi}{2}\). Also ist \(c=\frac{\pi}{2}\). Weiter sehen wir, dass sich der Graph der Funktion dreimal periodisch auf der Länge von \(2 \pi\) wiederholt. Damit ist \(b=3\). Mit der Amplitude \(a=0{,}75\) erhalten wir nach der allgemeinen Gleichung
\(\quad\) \( \begin{array}{ r c l} f(x) & = & a \cdot sin \Big( b \cdot (x -c) \Big) +d \end{array} \)
die Funktion
\(\quad\) \( \begin{array}{ r c l} f(x) & = & 0{,}75 \cdot sin\Big( 3 \cdot \big(x - \frac{\pi}{2} \big)\Big) + 1 \\ \end{array} \)
\(\\\)
Der aufmerksame Leser wird sehen, dass dies im Grunde eine Kosinusfunktion ist. Wir können auch sagen, das dies
\(\quad\) \( \begin{array}{ r c l} f(x) & = & 0{,}75 \cdot cos\big( 3 x \big) + 1 \\ \end{array} \)
ist.
\(\\\)
Auch hier folgt ein zweites Beispiel:
\(\quad\)

Wir zeichnen die Null-Linie ein.
\(\quad\)
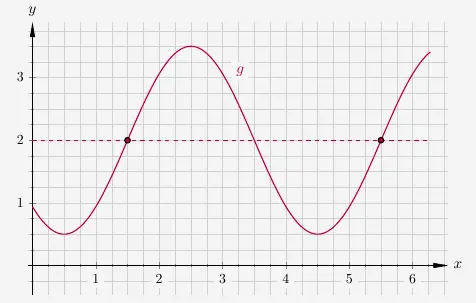
Wir haben einen Startwert bei \(c=1{,}5\) und eine Periodenlänge \(p=4\). Damit ist
\(\quad\) \( \begin{array}{ r c c c c c l } b & = & \frac{2 \pi}{p} & = & \frac{2 \pi}{4} & = & \frac{\pi}{2} \\ \end{array} \)
\(\\\)
Mit der Null-Linie \(d=2\) und der Amplitude \(a=1{,}5\) erhalten wir die Funktionsgleichung
\(\quad\) \( \begin{array}{ r c l} f(x) & = & 1{,}5 \cdot sin\Big( \frac{\pi}{2} \cdot \big(x - 1{,}5 \big)\Big) + 2 \\ \end{array} \)
\(\\[1em]\)